
Solved 11 A Find The Analytic Function F Z U Iv Chegg Com
The function f (x, y) satisfies the Laplace equation ∇ 2 f ( x, y) = 0 on a circular domain of radius r = 1 with its center at point P with coordinates x = 0, y = 0 The value of this function on the circularSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
U-v=(x-y)(x^2+4xy+y^2)
U-v=(x-y)(x^2+4xy+y^2)-2x = 6 x = 3 ∴ y = 4 Now, substitute x and y values in Start Learning English Hindi Home Now, substitute x1 Answer to Given (uv) =(xy)

2 Functional Dependence Pdf Differential Calculus Functions And Mappings
Solved (2y^{2} 2xy 3x)dx (y 4xy x^{2})dy = 0 Solve your problem for the price of one coffee Available 24/7 Math expert for every subjectCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyThe angle between the lines `x^(2)4xyy^(2)=0` is
Question Evaluate the expressions for x = 3 and y = 2 \sqrt {4 x^ {2}4 x yy^ {2}} 4x2 −4xy y2Stack Exchange network consists of 181 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build theirTransform the equation x^24xyy^22x2y4=0 into the form (y'^2)/(b^2)(x'^2)/(a^2)=1 Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P
U-v=(x-y)(x^2+4xy+y^2)のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
「U-v=(x-y)(x^2+4xy+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「U-v=(x-y)(x^2+4xy+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
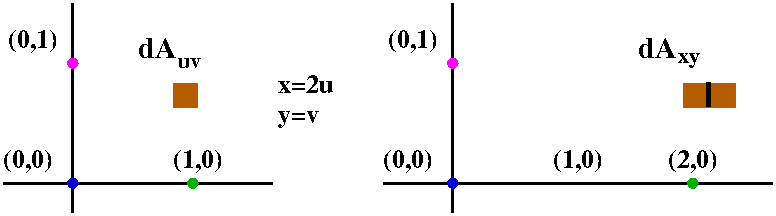 |  | |
 |  |  |
 |  |  |
「U-v=(x-y)(x^2+4xy+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「U-v=(x-y)(x^2+4xy+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
「U-v=(x-y)(x^2+4xy+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「U-v=(x-y)(x^2+4xy+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 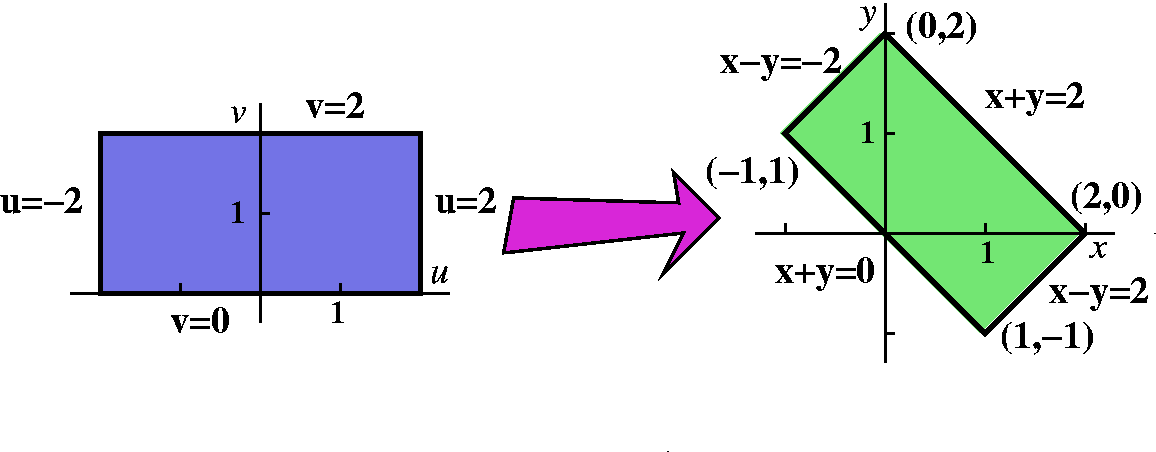 |  |
「U-v=(x-y)(x^2+4xy+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「U-v=(x-y)(x^2+4xy+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「U-v=(x-y)(x^2+4xy+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「U-v=(x-y)(x^2+4xy+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「U-v=(x-y)(x^2+4xy+y^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
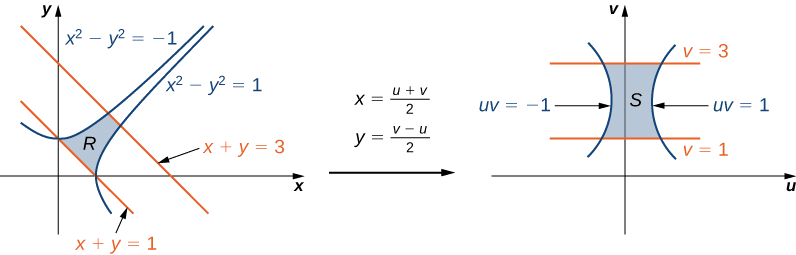
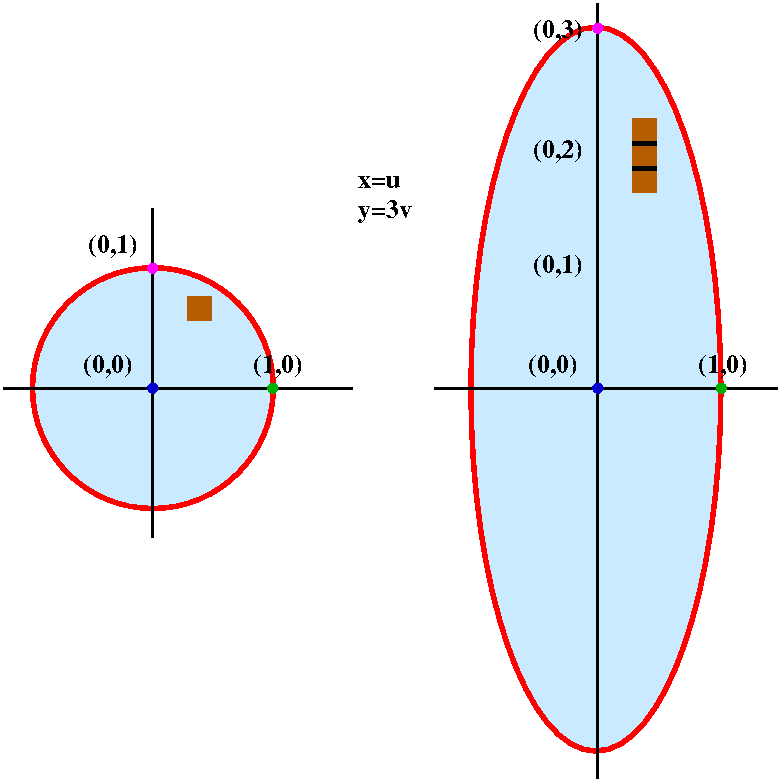
Moreover, the transformation (u;v) = T(x;y) = (3x2y;x−y) is onetoone and onto, as it must be in order to be a valid change of coordinates So 8 it has an inverse T−1 such that T T−1 =Identity v y = u x = 3 x 2 2 y − 4 y 2 and after integration v ( x, y) = 3 x 2 y y 2 − ( 4 / 3) y 3 β ( X) and after trying to solve for β I found it equal to β = x 2 y − x 2 and after applying it
Incoming Term: u-v=(x-y)(x^2+4xy+y^2),




0 件のコメント:
コメントを投稿